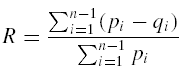RELMECS, diciembre 2015, vol. 5, no. 2, ISSN 1853-7863
Universidad Nacional de La Plata - Facultad de Humanidades y Ciencias de la Educación.
Centro Interdisciplinario de Metodología de las Ciencias Sociales.
Red Latinoamericana de Metodología de las Ciencias Sociales

ARTÍCULO / ARTICLE

Medida de concentración de Gini: observaciones sobre las fórmulas de cálculo y el Principio de Población de Dalton. Propuesta de un factor de corrección^*

Claudio Comari

Universidad Nacional de La Matanza
ccomari@hotmail.com
Argentina

Cita sugerida: Comari, C. (2015). Medida de concentración de Gini: observaciones sobre las formulas de cálculo y el principio de población de Dalton. Propuesta de un factor de corrección. Revista Latinoamericana de Metodología de las Ciencias Sociales, 5 (2). Recuperado a partir de: http://www.relmecs.fahce.unlp.edu.ar/article/view/relmecsv05n02a04

Resumen
En la primera parte del presente trabajo se investigan diferentes formas de cálculo de la razón de concentración conocida como Coeficiente o Índice de Gini, y el no cumplimiento del axioma conocido como de “invariancia a la replicación” o “Principio de Población de Dalton” en algunas de ellas. El alcance de las conclusiones se limita al comportamiento de las fórmulas sometidas a prueba (se encuentran entre las más conocidas) cuando son aplicadas a distribuciones de datos desagregados. En la segunda parte se propone un factor de corrección para las fórmulas de cálculo analizadas, de manera que satisfagan el Principio de Población.

Palabras Clave: Concentración; Curva de Lorenz; Medidas de desigualdad; Índice de Gini; Coeficiente de Gini; Principio de Población de Dalton.

Gini’s concentration measure: observations on the calculation formulas and Dalton’s Principle of Population
Proposal of a factor correction

Abstract
The first section of this paper will examine different calculations of the ratio of concentration known as Gini’s coefficient or index and the non-observance of the axiom known as "replication invariance" or "Dalton population principle" by someone of them. The reach of the conclusions is limited to the behavior of such formulas when applied to distributions of disaggregated data. The second part proposes a correction factor for the Gini coeffcient formulas analysed in order for them to fulfill the Dalton population principle.

Keywords: Concentration; Lorenz Curve; Inequality measures; Gini Index; Gini’s Coefficient; Dalton Population Principle.

Primera Sección

1. La razón de concentración propuesta por Gini

Entre las medidas de indicación de desigualdad en relación con el ingreso más utilizadas se encuentra el coeficiente o índice de Gini. La literatura es ambigua en la utilización de la nomenclatura: si bien todas las denominaciones refieren a la medición de la relación de las áreas del diagrama de Lorenz¹ algunos autores prefieren utilizar la denominación “Indice de Gini”², otros hablan del “Coeficiente de Gini”³ y están quienes utilizan ambas denominaciones de manera indistinta⁴, mientras que la denominación “Razón o Ratio de Concentración”⁵ -utilizada por el propio Corrado Gini⁶ al presentar la medida en su obra “Sulla misura della concentrazione e della variabilità dei caratteri” en 1914-, resulta menos frecuente.

A lo largo de este trabajo utilizaremos siempre la denominación “Medida de Concentración de Gini”, a pesar que los términos índice de Gini o coeficiente de Gini gozan de mayor familiaridad entre el público latinoamericano por ser las expresiones utilizadas por la Comisión Económica para América Latina y el Caribe (CEPAL) y las oficinas nacionales de estadística, entre otros actores relevantes.

En su artículo original Gini presenta su razón de concentración R:

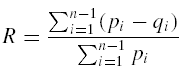(Gini, 1914:1207)

como un índice de concentración que satisface las siguientes condiciones:

a) aumenta al aumentar la concentración,

b) es igual a 1 en el caso de máxima concentración,

c) es igual a 0 en el caso de mínima concentración,

d) es el coeficiente que multiplicado por la fracción (p_i) de los casos en los cuales el carácter⁷ (la propiedad) presenta una intensidad inferior a un umbral dado, da el valor probable de la diferencia (p_i – q_i) entre su fracción y la fracción (q_i) de la cantidad total del carácter poseído por estos casos.

Creo conveniente señalar que el estadístico italiano ilustra su exposición con una diversidad de ejemplos prácticos y que aplica derivaciones de su fórmula a varias distribuciones de datos agrupados por frecuencias distintas de uno; es en esta ejemplificación que advierte que al reducirse el número de clases se reduce el resultado de R y que una misma distribución agrupada en el mismo número de clases pero con agrupaciones diferentes proporciona distintos valores de R’ y R’’.

Otro aspecto relevante de la propia presentación de Gini de su razón de concentración lo constituye su señalamiento de que con esta medida es posible proporcionar una medida exacta de la concentración de una propiedad, que tiene su correlato con el diagrama de Lorenz, cuya principal limitación resultaba de brindar una excelente representación gráfica de la concentración al mismo tiempo que conllevaba una extrema dificultad práctica para su precisa mensura.

Sintéticamente Gini resume sobre su artículo que:

a) propone un índice de concentración que es válido para cualquier propiedad independientemente de su distribución;

b) ha mostrado que su razón de concentración es una mejora del método gráfico propuesto por Lorenz;

c) la razón de concentración propuesta equivale a la diferencia media dividida 2 veces la media aritmética de la propiedad;

d) ha indicado los procedimientos aritméticos y gráficos convenientes para el cómputo de la razón de concentración

e) al haber considerado ejemplos de caracteres fisiológicos humanos tanto como propiedades económicas ha vinculado las teorías económicas de la concentración con las de los índices de variabilidad.

2. Medidas de desigualdad. Propiedades deseables: el enfoque axiomático

La proposición de atenerse a ciertos principios exigibles a las técnicas vinculadas al objeto de investigación y los valores subyacentes para confrontar los resultados de acuerdo al marco interpretativo de la investigación, obtuvo tal vez su mayor impulso en la orientación escogida por Dalton acerca de la medición de la desigualdad -en su caso partiendo de la consideración de que la reducción de la desigualdad de ingresos resulta deseable- (Dalton, 1920).

Casualmente la formulación de las propiedades exigibles a las medidas de desigualdad son formuladas por Dalton en su artículo “The Measurement of the Inequality of Incomes” (1920) en el que comenta y elogia las potencialidades de una medida propuesta por Gini en su obra “Variabilità e Mutabilità” (1912) a la que Dalton se refiere como “media relativa del Profesor Gini” y resulta un antecedente de la medida de concentración a cuyo análisis estamos abocados.

Lo cierto es que se trata de un debate que sigue vigente en términos de cuáles son los axiomas o principios deseables y las técnicas óptimas para ajustarse a ellos, y que la importancia de esta discusión a la vez condicionó definitivamente la utilización de técnicas estadísticas. De manera tal que en la actualidad es prácticamente imposible pensar la selección de técnicas de análisis en el campo de la distribución de rentas, desvinculada del marco interpretativo que justifica su uso.

A la fecha existe un importante consenso sobre los principios o condiciones exigibles a las medidas de desigualdad; entre ellos se destacan los requisitos de:

• ser invariantes a los cambios de escalas,

• cumplir el principio de transferencias de Pigou-Dalton, es decir que al producirse una transferencia desde una unidad situada en la parte superior a una unidad situada en la parte inferior de la escala, el indicador debe reflejar una disminución de la concentración,

• ser simétricas, de modo que el intercambio o permutación de rentas entre unidades no altere la medida,

• ser invariantes frente a la replicación de la población, principio que de ahora en más llamaremos Principio de Población de Dalton⁸ -aunque la literatura proporciona además otras denominaciones como se verá en el siguiente apartado-.

3. La Medida de Concentración de Gini frente al Principio de Población

En la profusa literatura sobre la temática son numerosos los autores⁹ que subrayan sin vacilación ni observaciones que la Medida de Concentración de Gini sí satisface la mencionada propiedad de invariancia ante la replicación de poblaciones, propiedad cuyo cumplimiento pondremos en cuestión respecto de algunas fórmulas de cálculo del conocido indicador; es de destacar que dicha afirmación se realiza apelando a una importante variedad de denominaciones del axioma o principio de marras: axioma de homogeneidad respecto a la población (Pascual Sáez, 2004); axioma de invariancia a la población (Metlika et al., 2005); axioma de invariancia a la replicación (Jan Goebel, 2007), (Osberg y Xu, 2007), (Salas, 1997), (Subramanian, 2004); axioma de la réplica de la población (Salas, 2001); criterio de población (Carrillo-Huerta y Vázquez Mateos, 2005); independencia de tamaño de la población (Goerlich, 1998 y 1999); independencia de tamaño o independencia a la replicación de la población (Medina, 2001); invariancia a la replicación (Osberg y Xu, 2000); irrelevancia poblacional (Duro, 2002); principio de adición proporcional de personas de Dalton (Kakwani, 1980); principio de invariancia a la población (Duclos et al., 2003); principio de población (Amarante, 2006), (Calderón Cuevas, 2006), (Cowell, 1998 y 2000); principio de réplicas poblacionales de Dalton (Cantó Sanchez et al., 2001), (Gradín y Del Río, 2001); constancia de la duplicación (Foster y Sen, 2001) o propiedad de invariancia de replicación (Foster et al., 2003).

En la revisión de la literatura hemos encontrado señalamientos -además de los presentados por el propio Gini- sobre limitaciones e imprecisiones de las fórmulas que utilizaremos en el presente trabajo ante ciertos tipos de distribuciones, por ejemplo, desaconsejando su utilización para distribuciones de muestras ponderadas¹⁰ y para datos agregados¹¹. Sin embargo no hemos registrado observaciones de alteraciones en los valores de la Medida de Concentración de Gini ante la replicación de la población cuando se trata de datos no agregados.

4. Metodología

Para demostrar que algunas fórmulas de cálculo de la Medida de Concentración de Gini no cumplen satisfactoriamente la propiedad del Principio de Población de Dalton aplicadas sobre distribuciones de población no agregadas, se presentarán ejemplos prácticos con poblaciones replicadas sobre los que se calculará el valor de la medida que ponemos a prueba. Asimismo se demostrará que las distribuciones mantienen idénticas medidas de tendencia central y de dispersión.

Las fórmulas de cálculo serán:

¹²

y

¹³

Las fórmulas con las que trabajaremos pueden presentarse con ligeras variaciones en la notación de los términos según los autores. Si bien a lo largo del trabajo se conservará la notación precedente por ser más frecuente, se considera que en todos los casos debería sustituirse n por N, ya que, como se expresó con anterioridad, no son fórmulas aplicables a distribuciones de datos agregados ni muestrales si pretenden obtenerse resultados exactos.

Solo para ejemplificar se presentan facsímiles de algunas notaciones:

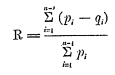
en Gini (1914),

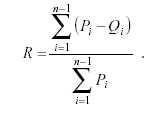
en Basulto Santos y Romero García (2003),

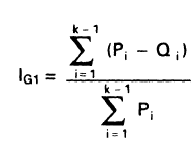
en Ferreira,y Garín,(1997), o

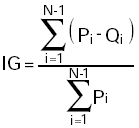
en Montero Lorenzo (2003).

5. Cómputos

5.1 Primera fórmula

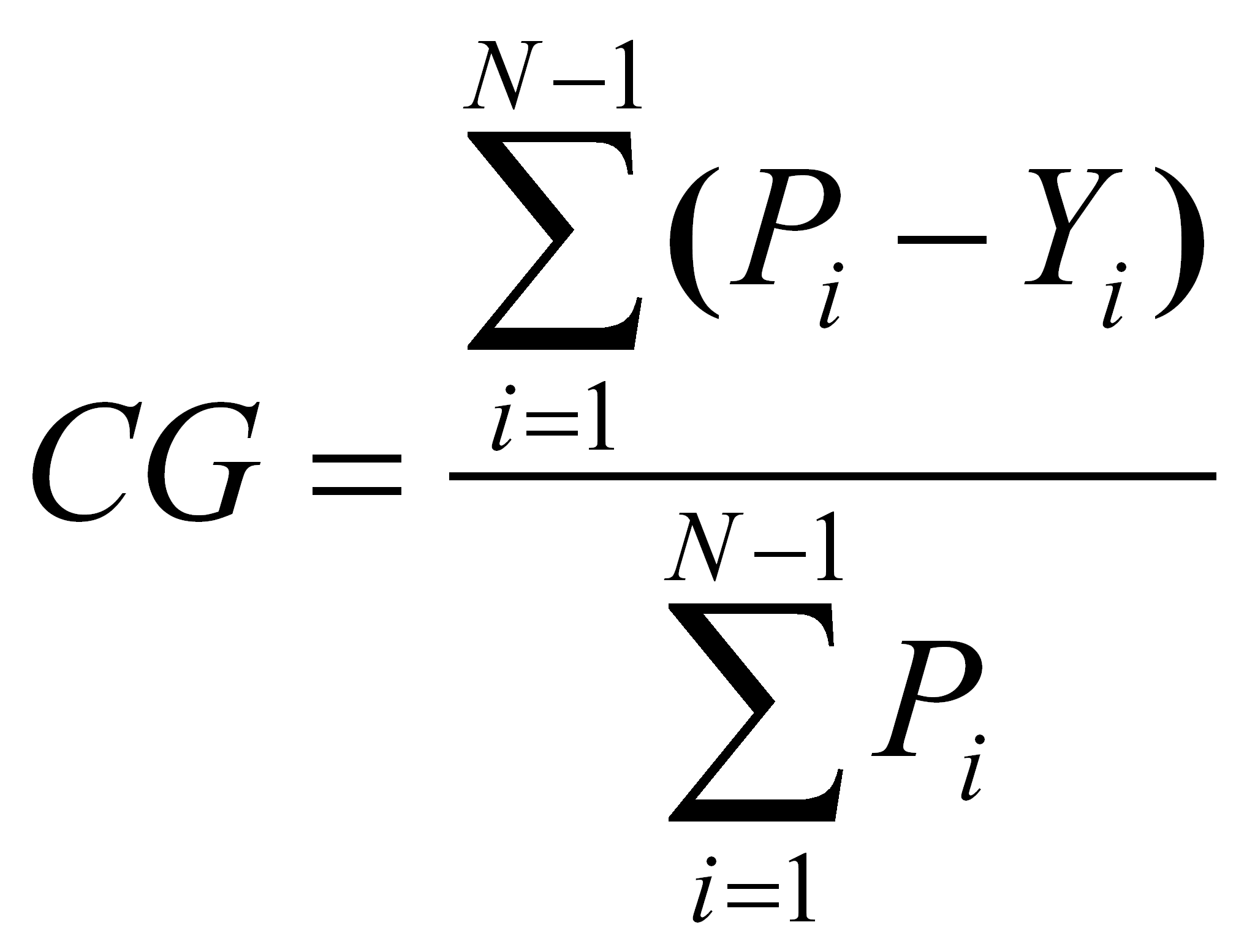(Medina, 2001)

pi , Pi : la distribución de frecuencias relativas simple y acumulada de la población bajo estudio

yi e Yi.: la distribución de frecuencias relativas simple y acumulada del ingreso de la unidad (perceptor, hogar, etc.).

La fórmula presentada es una de las más difundidas en los estudios metodológicos consultados. Aunque con notación equivalente, es la fómula originalmente presentada por Gini (Gini, 1914 y 2005), (Basulto Santos, 2003).

Recordamos que para la estimación de la Medida de Concentración de Gini con esta fórmula para datos desagregados se requiere del ordenamiento creciente de las unidades:

Referencias: Medina (2001, Cuadro 2, pp. 23-24).

El primer ejemplo se basa en una tabla -que se presenta a continuación- construida por Fernando Medina para la que se estimó la Medida de Concentración de Gini de los hogares a partir del ingreso total de cada hogar (Medina, 2001: 23-24). El cálculo se hizo sobre la distribución desagregada y sin ponderaciones. Las columnas “Tamaño del Hogar” e “Ingreso per Cápita” no tienen otra función que la de reproducir fielmente la tabla original.

Ejemplo N.° 1

Para esta tabla los términos de la fórmula son:

Para esta muestra de 30 casos la Medida de Concentración de Gini (calculado sobre el Ingreso Total Familiar) es igual a 0,8460.

Vamos a hacer de cuenta que contamos con tres dominios que replican los casos de nuestra primera tabla: el dominio N.° 1 cuenta con 300 casos (10 con cada valor de la tabla N.° 1); el dominio N.° 2 cuenta con 600 casos (20 con cada valor de la tabla N.° 1) y el dominio N.° 3 tiene 1200 casos (40 con cada valor de la tabla N. ° 1). Los resultados son los siguientes:

para el dominio N.° 1

MCG=0,8205;

para el dominio N.° 2

MCG= 0,8191;

y para el dominio N.° 3

MCG= 0,8184.

Nótese que para todas las distribuciones presentadas la media es $4.234,53, el mínimo es $25 y el máximo $69.845. Por lo tanto otras medidas frecuentemente usadas para el análisis de la distribución de la renta como el rango, la varianza, el coeficiente de variación y la razón de Kustnetz son idénticas para las distintas distribuciones presentadas.

Asimismo, si se calcularan los respectivos resultados de Gini sobre los mismos datos pero agregados en escalas de cuantiles, el valor sí se mantendría invariante.

5.2 Segunda fórmula

Se presenta a continuación otra de las fórmulas citadas con frecuencia, poniéndola a prueba respecto del ajuste a la invariancia ante la replicación.

Esta fórmula se deriva de la medida que Gini presentara como diferencia media en 1912 (y que Dalton ponderara en 1920), que es el promedio de las diferencias absolutas entre todos los pares con (N (N-1) pares).

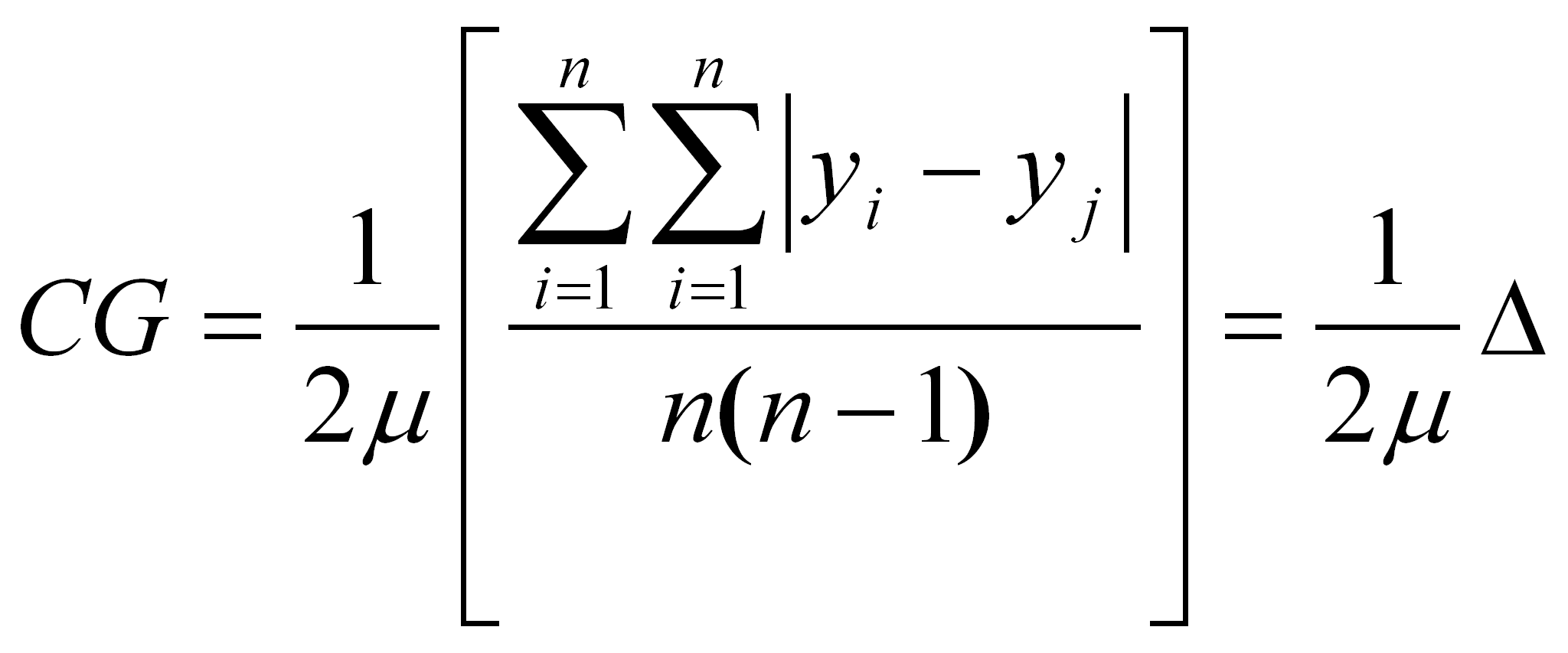(Medina, 2001)

En ésta fórmula  representa la media aritmética de las n(n-1) diferencias absolutas de las observaciones y 2 es el valor máximo que asume  cuando un individuo concentra todo el ingreso.

A fin de demostrar la equivalencia entre las fórmulas presentadas volvemos a trabajar sobre la primera tabla del ejemplo N.° 1 y obtenemos:

El resultado final es idéntico al obtenido con la primera fórmula.

Para observar si, como esperamos, se comportan igual frente a la replicación de poblaciones utilizaremos tablas más pequeñas para facilitar los cálculos de las diferencias absolutas de los pares posibles de ingresos.

Nuestra tabla tiene solo nueve perceptores de ingresos, con lo cual:

Para nuestra primera fórmula los resultados serán:

MCG= 0,4588

Para nuestra segunda fórmula los resultados serán:

Si replicamos la tabla anterior los resultados que obtendremos serán:

MCG= 0,4318

Y para nuestra segunda fórmula los resultados serán:

6. Primeras conclusiones

Como resumen, en el primer ejemplo obtuvimos:

Y para el segundo ejemplo

Hemos observado que ambas fórmulas son equivalentes ya que arrojan el mismo resultado respecto de cada tabla.

Asimismo, hemos podido observar que ante la replicación de la población la Medida de Concentración de Gini calculada con las fórmulas presentadas indefectiblemente varía, con lo cual consideramos definitivamente probado que dichas expresiones no cumplen el axioma de invariancia a la replicación o Principio de Población de Dalton.

Contextualizando ese enorme aporte de Corrado Gini vale señalar, por una parte, que su artículo antecede en varios años al de Dalton y su formulación axiomática, y que el cumplimiento del Principio de Población no aparece entre sus preocupaciones; incluso en forma reiterada valora como apropiado el uso de fórmulas que proporcionan valores aproximados al verdadero valor de R (motivado, presumiblemente, en el volumen de trabajo que comportaban los cálculos en la época). Por otra parte, la variabilidad ante la replicación está implícita en las observaciones que Gini realiza en su artículo, donde precisa la relación existente entre la medida propuesta y el método gráfico para la medición de la concentración utilizado por Lorenz, Chatelain y Séailles, que en la actualidad conocemos como Gráfico de Lorenz:

“...considérese para el diagrama siguiente (...), en el cual es n=14. Los n-1 pequeños rectángulos limitados por el eje de las abcisas y de la

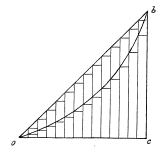
curva de concentración tienen la altura = q_i y la base = ; la suma de sus áreas será =. Los n-1 pequeños rectángulos limitados por el eje de las abcisas y por la recta de equidistribución tienen la base = y la altura = p_i, porque cada una de las ordenadas forma con la recta de equidistribución y con el eje de las abcisas un triángulo isósceles: la suma de sus áreas será = . La diferencia entre las dos sumas = será igual a la suma de las áreas de los n-1 rectángulos limitados por la recta de equidistribución y de la curva de concentración. Ahora, con el aumento de n, disminuye el área de la pequeña superficie comprendida entre la recta de equidistribución y la cúspide del rectángulo de altura p_i y análogamente disminuye el área de la pequeña superficie comprendida entre la curva de concentración y la cúspide del rectángulo de altura q_i . Con el aumento de n, el área del triángulo o b c tiende por lo tanto a devenir =, el área de concentración a devenir=

y la razón de concentración 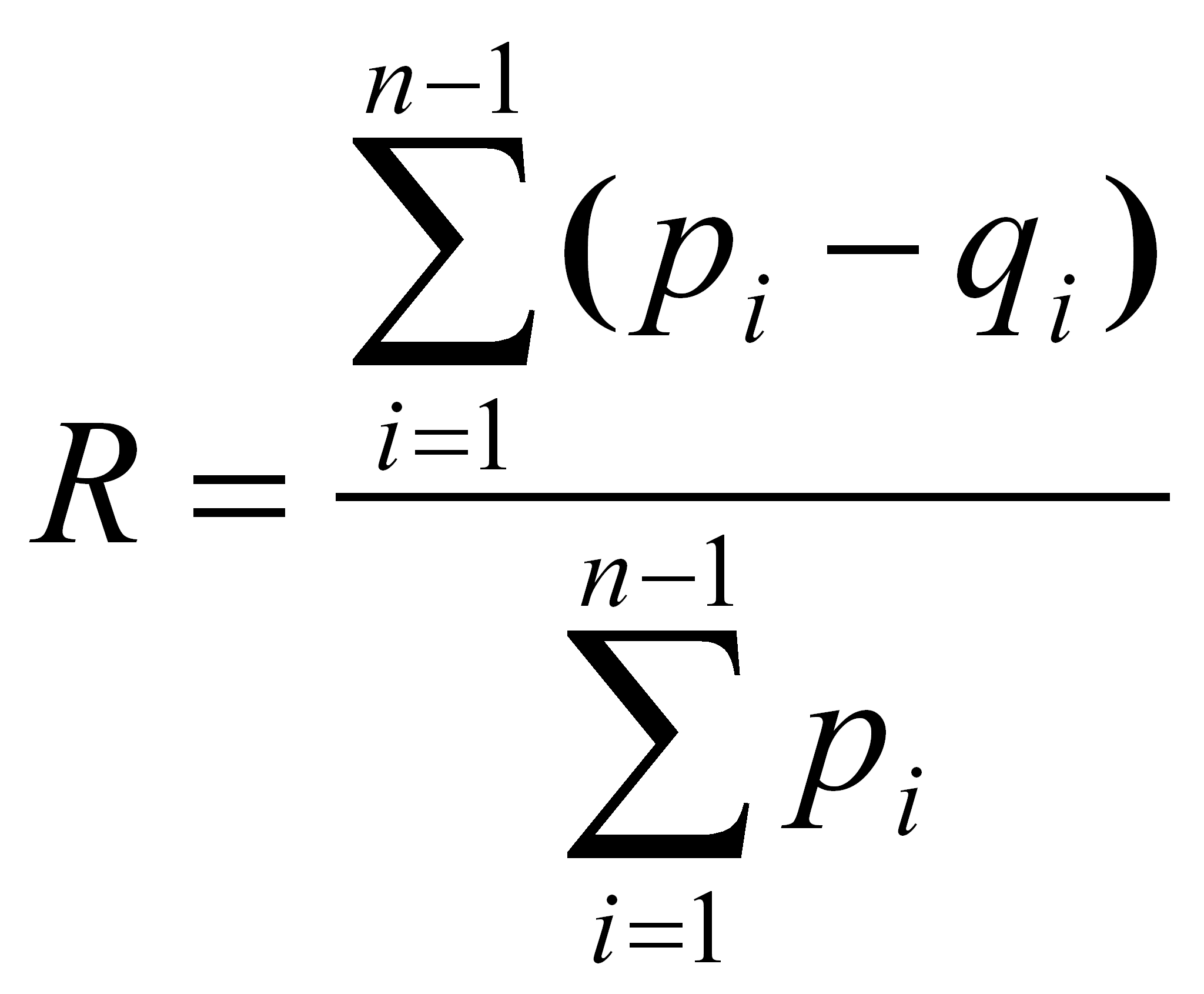.”¹⁴

Queda un importante campo de investigación a recorrer en esta relación entre el enfoque axiomático y la Medida de Concentración de Gini. Antes de terminar plantearemos en la próxima sección otra problemática vinculada a este tema.

Segunda Sección

7. Factor de corrección

Sobre la fórmula presentada en segundo término, señalaremos que puede arrojar resultados estables ante la replicación de la población si la normalización de la sumatoria de las diferencias absolutas entre los pares de valores se realiza con N² en lugar de N(N-1). Esa variante en la notación es la utilizada, entre otros, por Sen (1973) y Carrillo-Huerta et al. (2005) y se basa en la diferencia media relativa con repetición¹⁵ de Gini (1912):

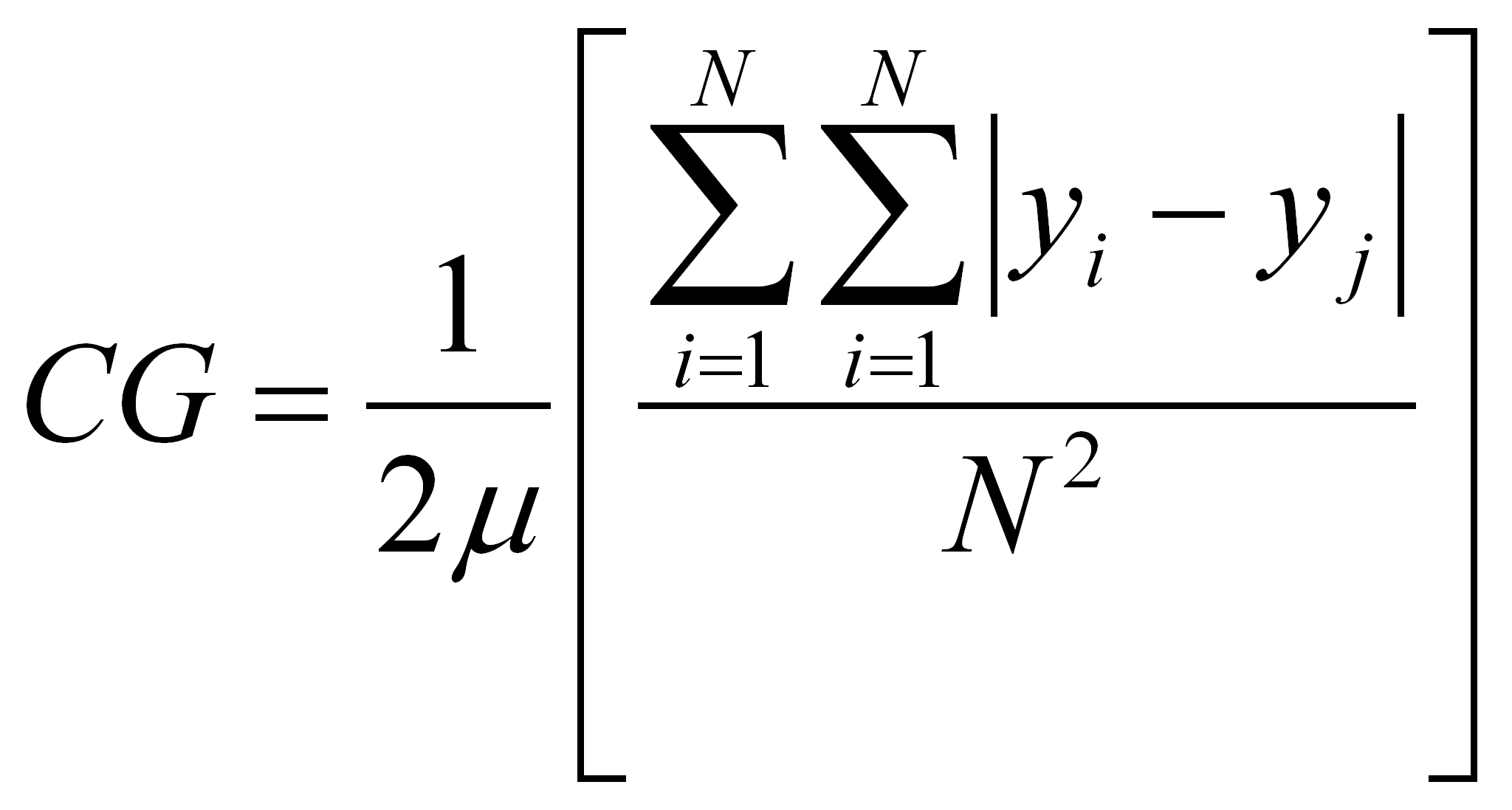
En efecto, recordemos que para el último ejemplo presentado:

Los resultados serán:

Pero si el cociente de las diferencias absolutas entre los pares de valores se obtiene a partir de N² en lugar de N(N-1):

Vemos que en este caso el resultado es estable ante la replicación de la población, aunque es significativamente menor a los obtenidos con las fórmulas originalmente contrastadas. Los mismos resultados se obtienen para todas las fórmulas equivalentes a las fórmulas 1 y 2 del presente trabajo si se multiplica el resultado de la Medida de Concentración de Gini por la expresión (o su equivalente: N-1/N) como factor de corrección por población finita.

Sintéticamente se presentan las fórmulas originales y corregidas por el factor de corrección y los resultados obtenidos para el último ejemplo:

Fórmula	N = 9	N = 18	Satisfacción del Principio de Población
	MCG= 0,4588	MCG= 0,4318	NO
	MCG= 0,40778152	MCG= 0,40778152	SI
	MCG= 0,4588	MCG= 0,4318	NO
	MCG= 0,40778152	MCG= 0,40778152	SI

8. Magnitudes del factor de corrección

Se desprende de la fórmula del factor de corrección que a medida que N crece el factor se aproxima a 1 (dado que la diferencia relativa entre ambas fórmulas tenderá a 0 pues si ), de manera que las diferencias observadas en los resultados de estas fórmulas de cálculo de Medida de Concentración de Gini ante distribuciones de datos no agregados de poblaciones replicadas serán despreciables para los N grandes.

Cuando las unidades de análisis son hogares o personas, generalmente el tamaño de la población es grande y, por tanto, las diferencias despreciables. Distinto es el caso de otras unidades de análisis, por ejemplo, las geopolíticamente determinadas, frecuentemente usadas por organismos multilaterales como los dependientes del sistema de Naciones Unidas.

Como ejemplo se presenta una tabla extraída del boletín de la Pan American Health Organization (PAHO, 2001: 3-4):

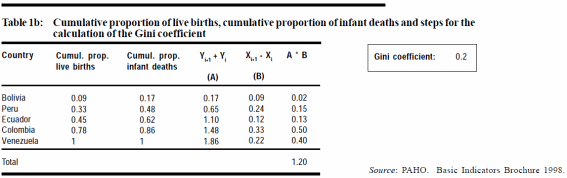
El estudio citado estima la desigualdad respecto de la mortalidad infantil en el área andina, con solo 5 casos. A la sazón, advertimos que la fórmula utilizada en la tabla anterior, conocida como Fórmula de Brown, es equivalente a las dos fórmulas puestas a prueba en el presente trabajo corregidas por el factor de corrección (PAHO, 2001: 3-4).

Volvemos a poner el foco en la magnitud esperable del factor de corrección, para lo cual presentamos a continuación una tabla para la que se calcula el valor del factor de corrección según el tamaño de N.

Sin embargo resulta conveniente tener en cuenta que, a la magnitud de la discrepancia entre los valores absolutos de las Medidas de Concentración de Gini, el tamaño de la población aporta un factor proporcional y por lo tanto las diferencias absolutas serán mayores a mayor desigualdad en la distribución, es decir a medida que el valor de Gini se aproxima a 1.

Presentamos a continuación tres tablas para 3 diferentes valores de Medida de Concentración de Gini obtenidos, conteniendo las Medidas de Concentración de Gini corregidas por el Factor de Corrección, y las diferencias absolutas entre las dos primeras medidas.

Sintéticamente, podemos afirmar que:

• El cálculo de las Medidas de Concentración de Gini con las fórmulas puestas a prueba no es independiente del tamaño de la población.

• La diferencia observada entre los resultados de esas fórmulas y las fórmulas normalizadas (que sí cumplimentan el axioma) indican que las primeras sobrestiman la desigualdad.

• La sobrestimación disminuye conforme crece el tamaño de N hasta hacerse despreciable.

• La sobrestimación en valores absolutos es mayor conforme aumente la desigualdad de la distribución.

Reflexiones

La diferencia en los resultados obtenidos responde a que en rigor estamos hablando de dos medidas distintas a las que la literatura ha confundido como única a partir de una nomenclatura confusa y un escaso rigor lingüístico; este problema reviste mayor gravedad cuando se toma en consideración que en la investigación empírica no siempre el investigador conoce que no todas las fórmulas obtienen el comportamiento esperado frente a diferentes características de las fuentes de datos, según sean datos de distribuciones de frecuencias simples, datos presentados en frecuencias mayores que 1 o datos agregados.¹⁶

La medida expresada a través de las fórmulas que presentan resultados variables ante la replicación responde a diferentes desarrollos de la fórmula de la Medida de Concentración de Gini, medida distinta de la expresada mediante aquellas fórmulas que proporcionan resultados idénticos y por tanto se ajustan a las pretensiones del enfoque axiomático.

Como mencionáramos anteriormente, el propio Gini relaciona su razón de concentración con la diferencia media; en el caso del primer grupo de fórmulas para la diferencia media el numerador es mientras que el denominador es N(N-1); el segundo grupo de fórmulas basado en la diferencia media con reposición conserva el mismo numerador que mientras que el denominador pasa a ser N². Las relaciones entre ambos desarrollos exceden los objetivos del presente informe y son abordados en otro artículo en preparación.

De tal manera queda presentado el desafío metodológico de construir una correcta tipología, que además de una nomenclatura unívoca de cada medida, dé cuenta de las propiedades de cada una de ellas y de cuáles son las fórmulas adecuadas para cada tipo de distribución, ya que la relación entre el enfoque axiomático y las medidas de desigualdad necesariamente incluye la relación entre los desarrollos matemáticos y los tipos de distribuciones de datos a los que se apliquen, amén de la importancia del ordenamiento y correcto uso de las nomenclaturas y notaciones.

Notas

* Artículo basado en la tesis de Maestría en Metodología de la Investigación Social de la UNIVERSITA DEGLI STUDI DI BOLOGNA y de la UNIVERSIDAD NACIONAL DE TRES DE FEBRERO de Claudio Comari, bajo la dirección de Augusto Hoszowski.

1 Relación por cociente entre el área de concentración (delimitada por la recta de equidistribución y la curva de concentración) y el área de máxima concentración.

2 Denominación utilizada en: Amarante (2006); Barcena, Imedio, Parrado, y colabs. (2007) Basulto Santos y Romero García (2003); Dagum (2001); Domínguez Domínguez (2006); Duclos Abdelkrim (2006); Ferreira Garín (1997); Goerlich (1998); Goerlich (1999); Gradín Del Río(2001); Kakwani (1980); Mira (2003); Molina (2005); Montanari Monari (2005); Nuñez Velázquez (2006); Osberg Xu (2000); Osberg Xu (2007); Pascual Sáez (2004); Pascual Sáez y Sarabia Alegría (2001); Nuñez Velazquez (2000); Portilla (2006); Ruiz-Castillo (2007); Salas (1997); Salas (2001).

3 Denominación utilizada en: Atkinson (1999); Beccaria González (2006); Calderón Cuevas (2006); Carrillo-Huerta y Vázquez Mateos (2005); CEPAL (2001); Cowell (1998); Cowell (2000); Duro (2002); Foster, López-Calva, Székely (2003); Gasparini Sosa Escudero (1999); Imedio (2007); Kostzer Perrot Villafañe (2005); Litchfield (1999); Nuñez Méndez, Sánchez Torres (1998); Rosales Candelari Altamirano (1998); Rothschild Stiglitz (1973); Salazar (2001); Sen (2001); Sinha (2004).

4 Badenes Plá (2003); Basulto Santos (2003); Buchelli Furtado (2005); Sánchez Gradín Lago y Del Río Otero (2000); CEPAL (2001); Duclos, Esteban, Ray, D. (2003); Gangas Peiró (2003); Imedio Olmedo (2005); Imedio Olmedo y Bárcena Martín (2007); Imedio Olmedo y Pascual Sáez (2003); Jan Goebel (2007); Medina (2001); Metlika Niemand, Salvia, y colabs. (2005); Nina y Aguilar (1998); Petrecolla (1997); Rionda Ramírez (2004); Rodríguez (2004); Ruiz Muñoz, Sánchez Sánchez, (2006); Subramanian (2004); Xu (2004); CEPAL (2011).

5 Denominación usada en Montanari Monari (2005). Se lo menciona como nomenclatura original de Gini en Basulto Santos (2003).

6 Gini (1914; 2005).

7 Dice Alberto Marradi (1995): “Nel linguaggio degli statistici si direbbe: sul carattere ‘colore dei capeli’. Gli statistici parlano infatti di ‘carattere’ laddove sociologi e politologi parlano di ‘propietà (e anche, impropiamente, di di ‘variabile’), e gli psicologi di ‘tratto’.

8 Denominación usada en:
Barcena, Imedio, Parrado y colabs. (2007); Imedio (2005); Imedio, Bárcena (2007); Imedio, Pascual Sáez (2003); Litchfield, (1999); Nuñez Velázquez (2006); Pena Trapero, Callealta Barroso, Nuñez Velazquez (2000); Ruiz-Castillo (2007); Salazar (2001). Dalton lo presenta como “the principle of proportionate adittions to persons” en su artículo The measurement of the inequality of incomes de 1920.

9 Algunos de ellos son: Foster, López-Calva, Székely (2003); Kakwani (1980); Pena Trapero, Callealta Barroso, Nuñez Velazquez (2000); Medina (2001); Amarante (2006); Imedio (2005); Salazar (2001); Calderón Cuevas (2006); Metlika, Niemand, Salvia y colabs. (2005); Foster, Sen (2001).

10 Basulto Santos (2003). Montero Lorenzo (2003).

11 Basulto Santos (2003). Medina (2001).

12 Basulto Santos (2003); Basulto Santos, Romero García (2003); Gini (2005); Ferreira, Garín (1997); Imedio (2007); Medina (2001); Mira (2003); Montanari, Monari (2005); Portilla (2006); Montero Lorenzo (2003); Montiel, Rius, Barón (1997); Ruiz Muñoz, Sánchez Sánchez (2006); Muñiz (1998). La fórmula presentada se puede encontrar con ligeras variaciones en la notación de los términos según los autores.

13 Amarante (2006); Medina (2001); Dagum (2001); Kakwani (1980); Medina (2001); Pena Trapero, Callealta Barroso, Nuñez Velazquez (2000); Xu (2004). La fórmula presentada se puede encontrar con ligeras variaciones en la notación de los términos según los autores.

14 Gini (1914) p.p. 1232-1233. Traducción C.C.

15 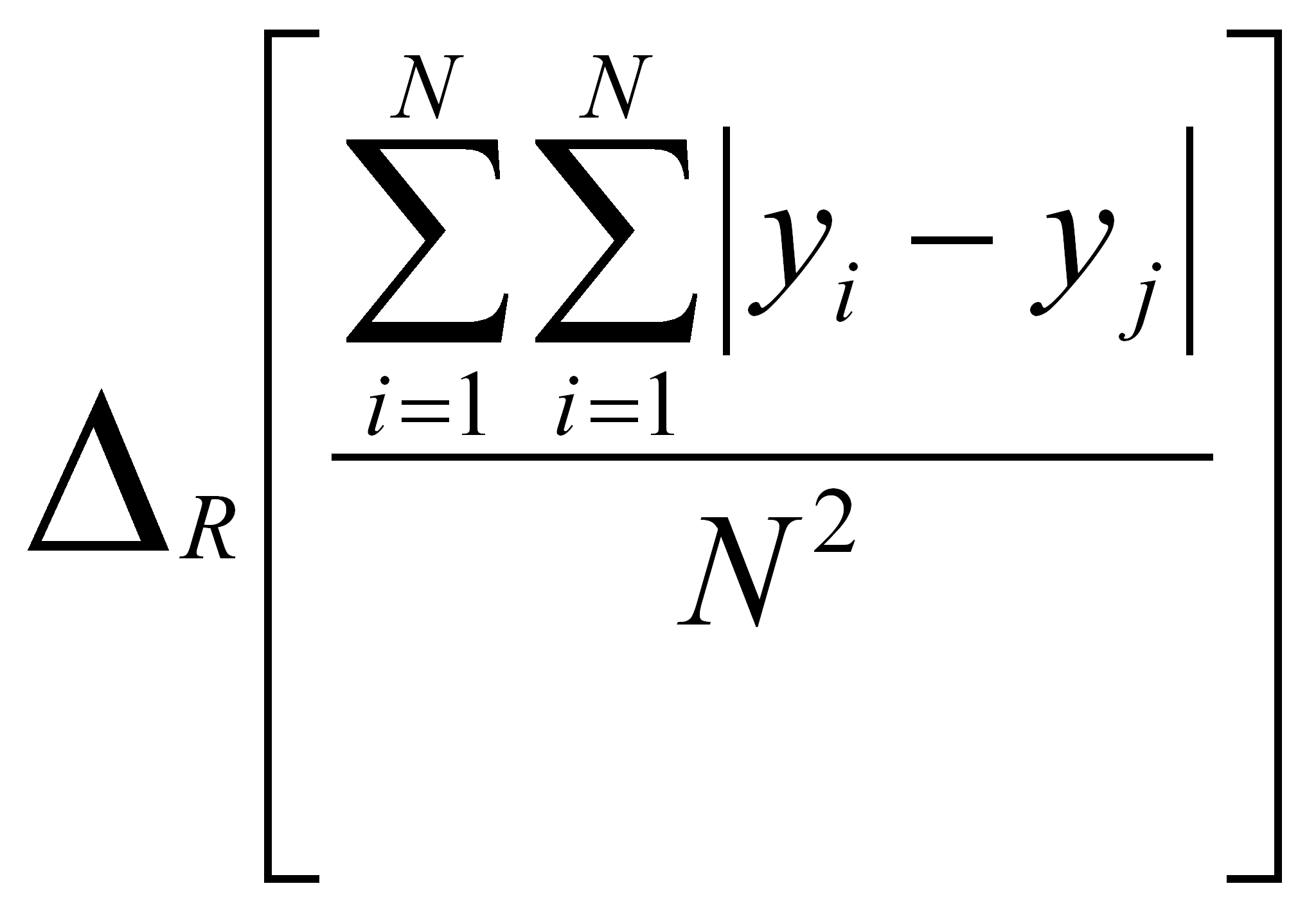Por tanto: sea la diferencia media relativa =, entonces la diferencia media con repetición es . (Gini, 1912, p.p. 22).

16 Basulto Santos (2003); Montero Lorenzo (2003); Medina (2001).

Bibliografía

Amarante, Verónica (2006). Desigualdad del ingreso. Conceptos y medidas.Apuntes elaborados para la Cátedra de Economía Descriptiva- Facultad de Ciencias Económicas y de Administración, 14 págs. Http://www.ccee.edu.uy/ensenian/catecdes/desigingamarante. PDF

Atkinson, Anthony Barnes (1999). Las contribuciones de Amartya Sen a la economía del bienestar. (Traducción de The contributions of Amartya Sen to Welfare Economics. Scandinavian Journal of Economics, vol. 101, issue 2.

Badenes Plá, Nuria (2003). Aproximación del Coeficiente de Gini con datos agrupados: límites inferior y superior y cálculos basados en bootstrap.

Barcena, Elena; Imedio, Luis J.; Parrado, Encarnación M. y colabs. (2007). La desigualdad en la Unión Europea, en el año 2000, a través de los índices de Gini, de Bonferroni y de De Vergottini. XIV Encuentro de Economía Pública. Málaga: Universidad de Málaga.

Basulto Santos, Jesús (2003). Problemas de agregación en el coeficiente de concentración de Gini -V Reunión de Economía Mundial. Sevilla

Basulto Santos, Jesús; Romero García, José Enrique (2003). Acerca de "Sulla misura della concentrazione e della variabilitá" de Corrado Gini. Almería, Asociación Española de Economía Aplicada, 31 págs.

Beccaria, Luis; González, Mariana (2006). Impactos de la dinámica de trabajo sobre la distribución del ingreso y la pobreza en Argentina. Problemas del Desarrollo, Vol. 37, N.º 146, pp. 97-120.

Buchelli, Marisa; Furtado Magdalena (2005) Uruguay 1998-2002: la distribución del ingreso en la crisis. Santiago de Chile: Revista de la CEPAL, N.º 86, pp. 167-82.

Calderón Cuevas, Eduardo (2006). El Ingreso Ciudadano como política alternativa para eliminar el trabajo infantil: reflexiones teóricas y presentación de un ejercicio cuantitativo de microsimulación. III Conferencia de la Red Latinoamericana y del Caribe

Cantó Sánchez, Olga; Gradín Lago, Carlos; Del Río Otero, Coral (2000). La Situación de los Estudios de Desigualdad y Pobreza en España. Vigo: Universidade de Vigo, pp. 36-88

Carrillo-Huerta, Mario M.; Vázquez Mateos, Haydee (2005). Desigualdad y polarización en la distribución del ingreso salarial en México.Problemas del desarrollo, vol. 36, 141, pp. 108-30.

CEPAL (2001) Características y tendencias de la distribución del ingreso. Panorama social de América Latina 2000-2001, pp.65-84.

CEPAL (2001). El uso de indicadores socioeconómicos en la formulación y evaluación de proyectos sociales- Aplicación metodológica.Santiago de Chile: Instituto Latinoamericano y del Caribe de Planificación Económica y Social-ILPES, 111 págs.

CEPAL (2011) Pobreza, desigualdad y ciclo de vida. Panorama social de América Latina 2010, pp.11-24.

Cowell, Frank (1998). Measurement of inequality. London: STICERD, London School of Economics and Political Science. 100 págs.

Cowell, Frank (2000). Measuring inequality. London: STICERD, London School of Economics and Political Science. 203 págs.

Dagum, Camilo (2001). Desigualdad del rédito y bienestar social, descomposición, distancia direccional y distancia métrica entre distribuciones. Madrid: Estudios de Economía Aplicada, vol. 17, N.° 001, pp. 5-52

Dalton, Hugh (1920).The measurement of the inequality of incomes.The Economist Journal, Vol. 30, N.° 119: pp. 348-61

Domínguez Domínguez, Juana; Martín Caravallo, Ana M. (2006). Medición de la pobreza: una revisión de los principales indicadores. Revista de métodos cuantitativos para la economía y la empresa. pp. 27-66.

Duclos, Jean-Ives; Abdelkrim, Araar (2006 ). Poverty and Equity - Measurement, Policy and Estimation with DAD. New York: Springer, New York: pp. 19-33.

Duclos, Jean-Ives; Esteban, Joan; Ray, Debraj (2003). Polarization: concepts, measurement, estimation. Centre interuniversitaire sur le risque, les politiques économiques et l’emploi, Cahier de recherche/Working Paper 03-01, 44 págs.

Duro, Juan Antonio (2002). Ensayos empíricos sobre desigualdades regionales. Universitat Autonoma de Barcelona, Departament d'economia aplicada, Tesis Doctoral, 332 págs.

Ferreira, Eva; Garín, Araceli (1997). Una nota sobre el cálculo del índice de Gini. Estadística Española, vol. 39, N.° 142, pp. 207-218.

Fidelli, Roberto (1998). La comparazione. Milano: FrancoAngeli, Metodologia delle scienze umane, 302 págs.

Forera Perilla, Andrés (s/d). Bienestar, pobreza y exclusion: la dimensión humana de la pobreza.

Foster, James E.; López-Calva, Luis F.; Székely, Miguel (2003). Medición de la Distribución del Desarrollo Humano: Metodología y su Aplicación en el caso de México.

Foster, James E.; Sen, Amartya K. (2001). “La desigualdad económica” después de un cuarto de siglo. México .Fondo de Cultura Económica.

Gamboa, Luis Fernando; Cortés Darwin (1999). Una Discusión en torno al concepto de Bienestar.Rosario: Universidad nacional de Rosario, serie Documenos, N.° 1, pp. 2-25.

Gangas Peiró, Pilar (2003).Desigualdad y pobreza. América Latina y Europa desde 1950 . Política y Cultura, N.º 20, pp. 29-51.

Gasparini, Leonardo; Sosa Escudero, Walter (1999). Bienestar y distribución del ingreso en la Argentina, 1980-1998.La Plata: Seminario Internacional de Federalismo Fiscal y Economías regionales. 24 págs.

Gini, Corrado (1912). Variabilità e mutabilità. Contibutto allo studio delle distruzione e delle relazione statistiche. Bologna. Tipografia di Paolo Cuppini. 164 págs.

Gini, Corrado (1914). Sulla misura della concentrazione e della variabilità dei caratteri, Atti del Reale Istituto Veneto di Scienze, Lettere ed Arti, 73(2), 1203-1248. (English translation in Metron, 2005, 63(1), 3-38).

Gini, Corrado (1914). Sulla misura della concentrazione e della variabilità dei caratteri, Atti del Reale Istituto Veneto di Scienze, Lettere ed Arti, 73(2), 1203-1248.

Gini, Corrado (1921). Measurement of Inequality of Incomes. The Economic Journal, Vol. 31, N.º 121, pp. 124-126.

Gini, Corrado (2005). On the Measurement of Concentration and variability of characters. METRON International Journal of Statistics, Vol. LXIII, N.º 1, pp. 3-38.

Goerlich, Francisco J. (1998). Desigualdad, diversidad y convergencia: (algunos) instrumentos de medida. Valencia: Instituto Valenciano de Investigaciones económicas, S.A., primera edición, 66 págs.

Goerlich, Francisco J. (1999). Dinámica de la distribución de la renta, 1955-1995: un enfoque desde la óptica de la desigualdad. Revista de estudios regionales, N.º 53, pp. 63-95.

Goerlich, Francisco J.; Mas, Matilde (1999). Desigualdad y Convergencia. Valencia: Instituto Valenciano de Investigaciones Económicas, S.A., 27 pags.

Gradín, Carlos; Del Río, Coral (2001). La medición de la desigualdad. Vigo: Universidade de Vigo, 46 págs.

 Imedio Olmedo, Luis (2005).Medición de la desigualdad a través de los momentos de la curva de Lorenz y de su curva dual .Estadística española Vol. 47, 158, pp. 89-115.

Imedio Olmedo, Luis J.; Bárcena Martín, Elena (2007). Dos familias numerables de medidas de desigualdad. Madrid: Investigaciones económicas, vol XXXI, 001, pp. 191-207.

Imedio Olmedo, Luis J. (2007). Algunas consideraciones sobre el Índice de Bonferroni .Estadística española. Vol. 49, Núm. 164, pp. 103 a 135.

Imedio Olmedo, Luis J.; Pascual Sáez, Marta (2003). Privación, status e imposición sobre la renta. Estudios de economía aplicada, vol. 21, 001, pp. 123-47.

Jan Goebel, M.A. (2007). Methodological Issues in the measurement of income and poverty. Berlín: genehmigte dissertation, 193 págs.

Kakwani, Nanak C. (1980).Income Inequality and Poverty Methods of Estimation and Policy Applications.Published for the World Bank by Oxford University Press, 416 págs.

Kostzer, Daniel; Perrot, Bárbara ; Villafañe, Soledad (2005). Distribución del ingreso, pobreza y crecimiento en la Argentina. Buenos Aires: Ministerio de Trabajo, Empleo y Seguridad Social, Subsecretaría de Programación Técnica y Estudios Laborales, 174 págs.

Litchfield, Julie A. (1999). Inequality: Methods and Tools.Text for the World Bank Poverty Net website: http://www.worldbank.org/poverty

Marradi, Alberto (1995). L' analisi monovariata. Milano: FrancoAngeli, Metodologia delle scienze umane, 180 págs.

Marradi, Alberto (1997). Linee guida per l'analisi bivariata dei dati nelle scienze sociali. Milano: FrancoAngeli, Laboratorio sociologico, 186 págs.

Medina, Fernando (2001). Consideraciones sobre el índice de Gini para medir la concentración del ingreso. Santiago de Chile: Serie Estudios estadísticos y prospectivos CEPAL ECLAC, 42 págs.

Metlika, Úrsula; Niemand, María Sol; Salvia, Agustín; y colabs. (2005). Desigualdad social y heterogeneidad regional en la Argentina. Un balance del período 1991-2001.Mar del Plata: Foro Trayectos y Territorios de Desempleo, 22 págs.

Mira, Antonietta (2003). Lez. 6 - Analisi dei dati. Universitá dell'Insubria. Facoltá di Economia. 15 págs. http://eco.uninsubria.it/webdocenti/amira/andati-www/2003/sei.pdf

Molina, Emiro A. (2005). La medición de la equidad: marco conceptual. 8 pags. http://redeconomia.org.ve/documentos/emolina.doc.

Montanari, Angela; Monari, Paola (2005). Gini’s contribution to multivariate statistical analysis. Bologna: Dipartimento di Scienze Statistiche Università di Bologna, Mimeo, 18 págs.

Montero Lorenzo, José María (2003). Sobre concentración económica: Índice E para colectivos discretos. Estadística española Vol. 45, Núm. 152, pp. 22-54.

Montiel, A. M.; Rius, F.; Barón, F.J. (1997). Elementos Basicos de Estadística Económica y Empresarial. Madrid. Prentice Hall, p.p. 102-107.

Nina, Esteban y Aguilar, Ana (1998). Amartya Sen y el estudio de la desigualdad económica y la pobreza monetaria. Colombia 1978-1997.Bogotá: Cuadernos de Economía, v. XVII, 29.

Nuñez Méndez, Sánchez Torres, Fabio (1998). Descomposición de la desigualdad del ingreso laboral urbano en Colombia: 1976-1997. República de Colombia: Departamento Nacional de Planeación, Unidad de Análisis Macroeconómico, Archivos de macroeconomía, doc 86.

Nuñez Velázquez, José Javier (2006). La desigualdad económica medida a través de la curva de Lorenz. Revista de métodos cuantitativos para la economía y la empresa, 2, pp. 67-108.

Osberg, Lars; Xu, Kuan (2000). Poverty durations and poverty measurement. Halifax, Nova Scotia: Dalhousie University, 35 págs.

Osberg, Lars; Xu, Kuan (2007). How should we measure poverty in a changing world? Methodological issues and Chinese case study. Halifax, Nova Scotia: Dalhousie University, 48 págs.

PAHO (2001). Measuring Health Inequalities:Gini Coefficient and Concentration Index. Pan American Health Organization. Epidemiological Bulletin / PAHO, Vol. 22, N.º 1, pp. 3 a 4.

Pascual Sáez, Marta (2004). Modelización estocástica de distribuciones de renta a partir de familias paramétricas. Tesis Doctoral, Instituto de Estudios Fiscales, 254 págs.

Pascual Sáez, Marta; Sarabia Alegría, J.M. (2001). Rankings de distribuciones de renta basados en curvas de Lorenz ordenadas: un estudio empírico 1. Estudios de economía aplicada, Vol. 19, N.º 03, pp. 151-69.

Pena Trapero, J.B.; Callealta Barroso, F.J.; Nuñez Velazquez, J.J. (2000) Encuestas de presupuestos familiares,renta de las familias y estudio de la distribución personal de la renta: una experiencia española. Universidad de Alcalá.

Petrecolla, Diego (1997). Distintas descomposiciones del coeficiente de Gini para el Gran Buenos Aires, 1980-1995. Bahía Blanca, XXXII Reunión Anual de la Asociación Argentina de Economía Política, 21 págs.

Pigou, Arthur C. (1932). The economics of welfare. London: Macmillan and Co., 4.° edición.

Portilla, Idoia (2006). 7° sesion: Medidas de concentración. Universidad de Navarra. P.p. 59-64. http://www.scribd.com/doc/4036664/sesion7 .

Rionda Ramírez, Jorge Isauro (2004). Algunas consideraciones en torno a cómo medir el nivel de bienestar social. 8 pags.http://www.eumed.net/ce/2004/jirr-bienestar.htm

Rodríguez, Juan Gabriel (2004). Measuring polarization,inequality, welfare and poverty. Madrid: Fundación Centro de Estudios Andaluces, 30 págs.

Rodríguez, Luis Mariano (s/d). Los índices de concentración - Una visión General. Superintendencia para la Promoción y Protección de la Libre Competencia. Ministerio del Poder Popular para las Industrias Ligeras y el Comercio. Gobierno Bolivariano de Venezuela. http://www.procompetencia.gov.ve/LOS%INDICES%20DE%20CONCENTRACION.pdf

Rosales, Gladys del Valle; Candelari, Gustavo E.; Altamirano, Marcelo L. (1998). Una medición de la distribución del ingreso el caso de Catamarca. Catamarca: Congreso de desarrollo regional, Tomo II, Sección desarrollo social, pp.1-8.

Rothschild, Michael; Stiglitz, Joseph (1973). Some further results on the measurement of Inequality. Belgium, Journal of Economic Theory, vol. 6, N° 2, p.p. 188-204.

Ruiz Muñoz, David; Sánchez Sánchez, Ana María (2006). Apuntes de estadistica, 113 págs. http://www.eumed.net/libros/2006a/rmss/index.htm

Ruiz-Castillo, Javier (2007). La medición de la desigualdad de la renta: una revisión de la literatura. Madrid: Universidad Carlos III de Madrid, Departamento de economía, Documento de trabajo, serie de economía 01, 44 págs.

Salas, Rafael (1997).Welfare-consistent inequality indices in changing populations: The marginal population replication axiom. A note.Journal of Public Economics 67, pp. 145-150.

Salas, Rafael (2001). La medición de la desigualdad económica. Instituto de Estudios Fiscales y Universidad Complutense de Madrid. 40 pags.

Salazar, Alberto N. (2001).Distribución del Ingreso y Bienestar en la Patagonia Austral, 199 -1999. 5.° Congreso Nacional de Estudios del trabajo. ASET, 18 págs.

Sen, Amartya (1995) Nuevo examen de la desigualdad. Alianza Editorial. p.p. 119-132.

Sen, Amartya K. (2001). La desigualdad económica. México .Fondo de Cultura Económica.

Sinha, S.P. (2004). Axiomas y Propiedades de medidas de pobreza. Mérida, U.L.A., 7 págs.

Subramanian, S. (2004). Indicators of Inequality and Poverty. United Nations University, Research Paper No. 2004/25, 27 págs.

Uriel, Ezequiel; Muñiz, Manuel (1998). Estadística Económica y Empresarial - Teoría y Ejercicios. Madrid. Editorial AC, pp. 45-49.

Xu, Kuan (2004). How has the literature on Gini's Index evolved in the past 80 years?. Nova scotia, 41 págs.

Recibido: 14 de marzo de 2014
Aceptado: 28 de agosto de 2014
Publicado: 9 de diciembre de 2015

Esta obra está bajo licencia
Creative Commons Atribución-NoComercial-CompartirIgual 3.0